KCL and KVL are the two basic electrical laws. One is used for current and the other is used for voltage. The name Kirchhoff came from the Scientist (Gustav Kirchhoff) himself. If you are seeking this information then you are at the right place.
Table of Contents
Kirchhoff’s Current Law (KCL)
KCL is also known as Kirchhoff’s first law. this is based on the law of conservation of charge, which requires that the algebraic sum of charges within a system cannot change.
KCL (Kirchhoff’s current law) states that the algebraic sum of currents entering a node (or a closed boundary) is zero. Mathematically, KCL implies that –
\sum_{n=1}^{N}i_{n}=0where N is the number of branches connected to the node and in is the nth current entering (or leaving) the node. By this law, currents entering a node may be regarded as positive, while leaving the node may be taken as negative or vice versa.
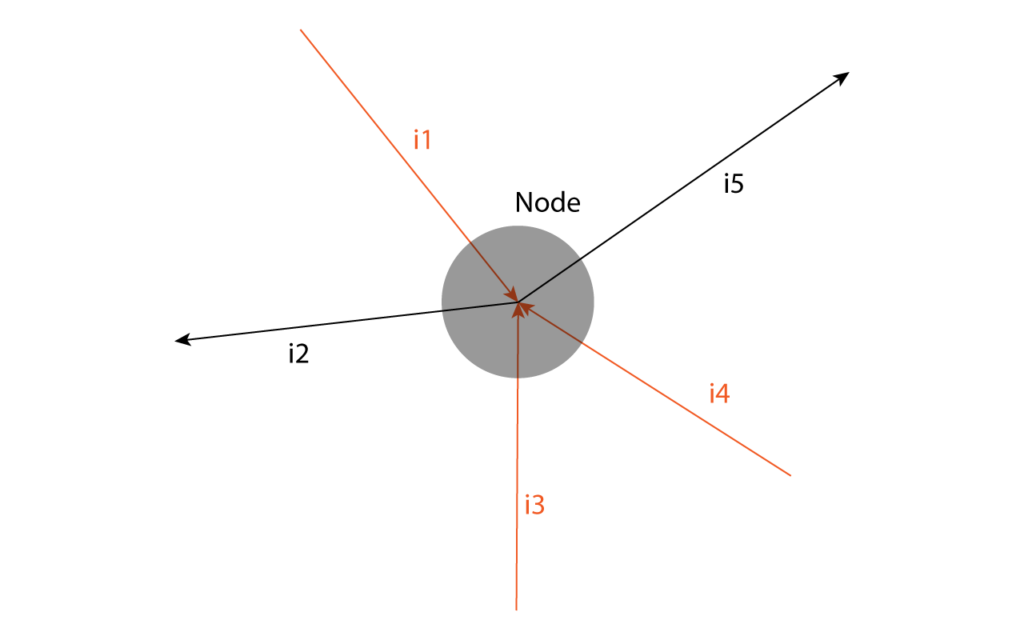
Consider the node in the above figure. Applying KCL gives:
i1+ (-i2) + i3 + i4 + (-i5) = 0
since currents i1, i3 and i4 are entering the node, while i2 and i5 are leaving it. By rearranging the terms we get:
i1 + i3 + i4 = i2 + i5
This is an alternative form of KCL.
KCL for a closed surface
In general, KCL applies to any closed boundary or surface. Since a node may be regarded as a closed surface shrunk to a point. In two dimensions, a closed boundary is the same as a closed path. For example, consider the below circuit.
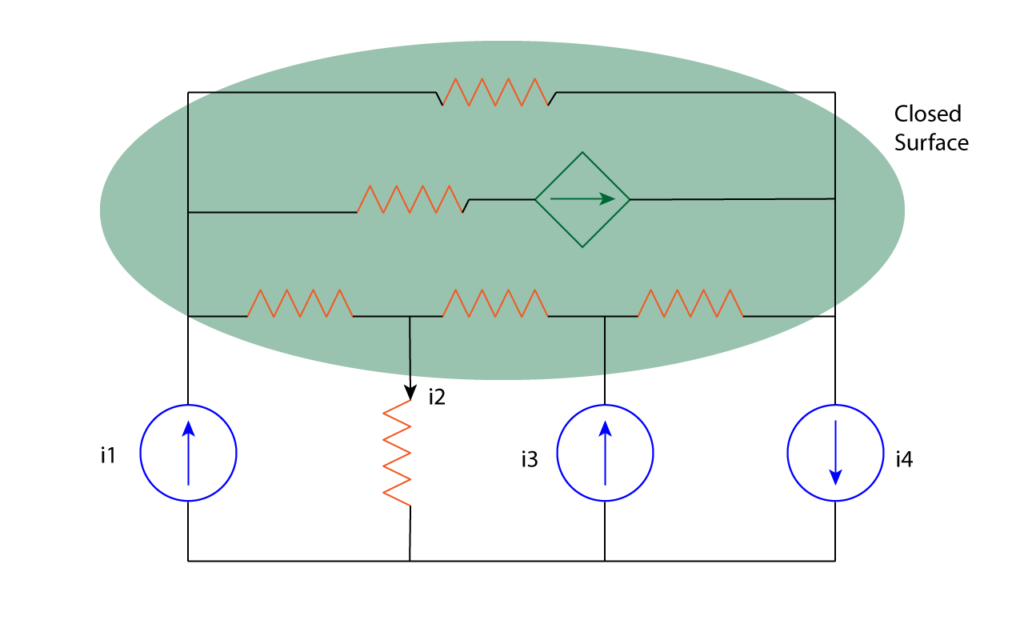
If we define a closed surface as shown in the figure and apply KCL as:
I1 + I3 = I2 + I4
Kirchhoff’s Voltage Law (KVL)
KVL is also known as Kirchhoff’s second law. This is based on the principle of conservation of energy. KVL states that the algebraic sum of all voltages around a closed path or loop is zero. Expressed Mathematically, KVL states that:
\sum_{m=1}^{M} V_m = 0where M is the number of voltages in the loop (or the number of branches in the loop) and Vm is the mth voltage.
Sign convention in KVL
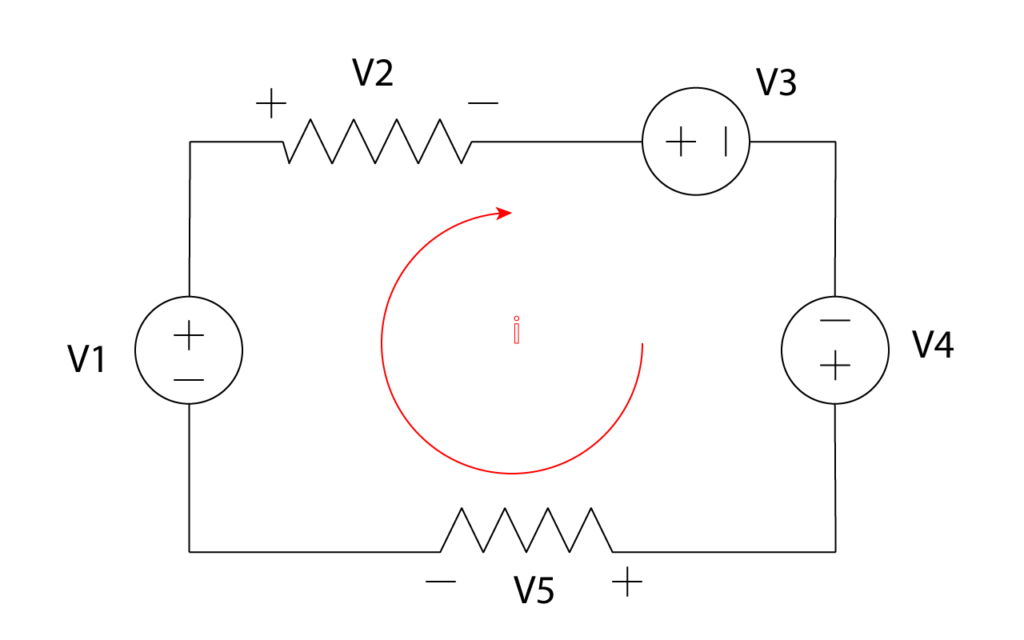
While moving around the loop in any direction (either clockwise or anti-clockwise), a plus sign is assigned to a potential rise (- to +), and a minus sign to a potential drop (+ to -). For example, consider the circuit of the above figure, where voltages V1 and V4 are taken positively as voltage rises and voltage V2, V3, and V5 are taken as negative drops. Writing KVL around a clockwise direction we get:
V1 – V2 – V3 + V4 – V5 = 0
∑Vdrop = ∑Vrise
V2 + V3 + V5 = V1 + V5
FAQs – Frequently Asked Questions
What is KCL?
KCL stands for Kirchhoff’s Current Law. It is a fundamental law in electrical engineering that states that the total current entering a node or junction in a circuit must be equal to the total current leaving that node or junction.
What is KVL?
KVL stands for Kirchhoff’s Voltage Law. It is another fundamental law in electrical engineering that states that the sum of all voltages around a closed loop in a circuit must equal zero.
What is the difference between KCL and KVL?
KCL deals with the conservation of current at a node or junction, while KVL deals with the conservation of energy around a closed loop in a circuit.
How are KCL and KVL used in circuit analysis?
KCL and KVL are used to derive equations that can be used to analyze and solve complex circuits. By applying these laws to various parts of a circuit, it is possible to determine the current and voltage at any point in the circuit.
What are some practical applications of KCL and KVL?
KCL and KVL are used in a wide range of practical applications, such as designing electronic circuits, analyzing power systems, and troubleshooting electrical problems.
What is a node in a circuit?
A node is a point in a circuit where two or more circuit elements are connected.
What is a loop in a circuit?
A loop is a closed path in a circuit that starts and ends at the same point, passing through one or more circuit elements.
Can KCL and KVL be applied to circuits with alternating current (AC)?
Yes, KCL and KVL can be applied to circuits with AC, but the analysis becomes more complex due to the varying current and voltage over time.
Are KCL and KVL the only laws in circuit analysis?
No, there are other laws and principles in circuit analysis, such as Ohm’s Law, the Superposition Principle, and Thevenin’s Theorem. However, KCL and KVL are fundamental and essential laws that form the basis of circuit analysis.